N-Queens II

Then-queens puzzle is the problem of placingn_queens on an_n×_n_chessboard such that no two queens attack each other.

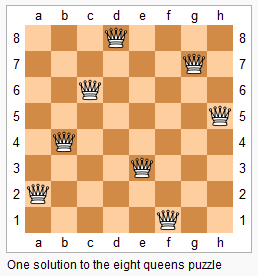
Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example:

Input:
 4

Output:
 2

Explanation:
 There are two distinct solutions to the 4-queens puzzle as shown below.
[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

Solution

The same as N-Queens, just need to output size of results.

class Solution {
    public int totalNQueens(int n) {
        List<List<Integer>> ans = new ArrayList<>();

        if (n <= 0) {
            return 0;
        }
        searchHelper(n, new ArrayList<Integer>(), ans);

        return ans.size();
    }

    // Backtracking recursively find the valid solutions
    private void searchHelper(int n, List<Integer> cols, List<List<Integer>> ans) {
        if (cols.size() == n) {
            ans.add(new ArrayList<Integer>(cols));
            return;
        }

        for (int col = 0; col < n; col++) {
            if (!isValid(col, cols)) {
                continue;
            }
            cols.add(col);
            searchHelper(n, cols, ans);
            cols.remove(cols.size() - 1);
        }
    }

    // Check if the new position to be placed is invalid
    private boolean isValid(int col, List<Integer> cols) {
        if (cols.size() == 0) {
            return true;
        }

        for (int row = 0; row < cols.size(); row++) {
            if (col == cols.get(row)) {
                return false;
            }
            if (cols.get(row) - row == col - cols.size()) {
                return false;
            }
            if (cols.get(row) + row == col + cols.size()) {
                return false;
            }
        }
        return true;
    }
}

Or just use a global variable

class Solution {
    private static int total;
    public int totalNQueens(int n) {
        List<List<Integer>> ans = new ArrayList<>();

        if (n <= 0) {
            return 0;
        }
        total = 0;
        searchHelper(n, new ArrayList<Integer>());

        return total;
    }

    // Backtracking recursively find the valid solutions
    private void searchHelper(int n, List<Integer> cols) {
        if (cols.size() == n) {
            total++;
            return;
        }

        for (int col = 0; col < n; col++) {
            if (!isValid(col, cols)) {
                continue;
            }
            cols.add(col);
            searchHelper(n, cols);
            cols.remove(cols.size() - 1);
        }
    }

    // Check if the new position to be placed is invalid
    private boolean isValid(int col, List<Integer> cols) {
        if (cols.size() == 0) {
            return true;
        }

        for (int row = 0; row < cols.size(); row++) {
            if (col == cols.get(row)) {
                return false;
            }
            if (cols.get(row) - row == col - cols.size()) {
                return false;
            }
            if (cols.get(row) + row == col + cols.size()) {
                return false;
            }
        }
        return true;
    }
}

有关全局变量：

@mnmunknown

既然不需要输出最终解，也就省去了传递 rst 和把棋盘转成 String 的过程。一个问题是，如何在这种dfs + backtracking中维护一个 primitive type 变量，比如有效解的总数？

Java 中默认 primitive type 是 pass by value，而且 Integer type 虽然作为一个 object 存在但是是 immutable, 不能用来作为全局参数多个函数共同更新。

直接建全局变量太蠢了，也不好看。

Not using global variable

public class Solution {
    public int totalNQueens(int n) {
        return dfs(0, n, new boolean[n], new boolean[2*n - 1], new boolean[2*n - 1]);
    }

    private int dfs(int row, int n, boolean[] cols, boolean[] diag45, boolean[] diag135){
        if(row == n){
            return 1;
        }

        int solutionCount = 0;
        for(int col = 0; col < n; col++){
            if(!cols[col] && !diag45[row + col] && !diag135[row - col + n - 1]){
                cols[col] = true;
                diag45[row + col] = true;
                diag135[row - col + n - 1] = true;

                solutionCount += dfs(row + 1, n, cols, diag45, diag135);

                cols[col] = false;
                diag45[row + col] = false;
                diag135[row - col + n - 1] = false;
            }    
        }
        return solutionCount;
    }
}