> For the complete documentation index, see [llms.txt](https://aaronice.gitbook.io/lintcode/llms.txt). Markdown versions of documentation pages are available by appending `.md` to page URLs; this page is available as [Markdown](https://aaronice.gitbook.io/lintcode/data_structure/insert-delete-getrandom-o1.md).

# Insert Delete GetRandom O(1)

`Dynamic Programming`, `Kadane's Algorithm`

Given a 2D array, find the maximum sum subarray in it. For example, in the following 2D array, the maximum sum subarray is highlighted with blue rectangle and sum of this subarray is 29.

[![](https://www.geeksforgeeks.org/wp-content/uploads/rectangle-11.png)](https://www.geeksforgeeks.org/wp-content/uploads/rectangle.png)

## Solution & Analysis

The **naive solution** for this problem is to check every possible rectangle in given 2D array. This solution requires 4 nested loops and time complexity of this solution would be O(n^4).

**Kadane’s algorithm** for 1D array can be used to reduce the time complexity to O(n^3). The idea is to fix the left and right columns one by one and find the maximum sum contiguous rows for every left and right column pair. We basically find top and bottom row numbers (which have maximum sum) for every fixed left and right column pair. To find the top and bottom row numbers, calculate sun of elements in every row from left to right and store these sums in an array say temp\[]. So temp\[i] indicates sum of elements from left to right in row i. If we apply Kadane’s 1D algorithm on temp\[], and get the maximum sum subarray of temp, this maximum sum would be the maximum possible sum with left and right as boundary columns. To get the overall maximum sum, we compare this sum with the maximum sum so far.

```java
import java.util.*; 
import java.lang.*; 
import java.io.*; 

/** 
* Given a 2D array, find the maximum sum subarray in it 
*/
class Ideone 
{ 
    public static void main (String[] args) throws java.lang.Exception 
    { 
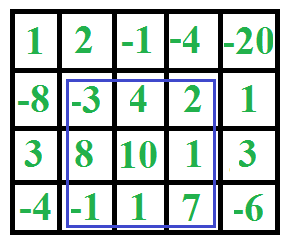
        findMaxSubMatrix(new int[][] { 
                            {1, 2, -1, -4, -20}, 
                            {-8, -3, 4, 2, 1}, 
                            {3, 8, 10, 1, 3}, 
                            {-4, -1, 1, 7, -6} 
                            }); 
    } 

    /** 
    * To find maxSum in 1d array 
    * 
    * return {maxSum, left, right} 
    */
    public static int[] kadane(int[] a) { 
        //result[0] == maxSum, result[1] == start, result[2] == end; 
        int[] result = new int[]{Integer.MIN_VALUE, 0, -1}; 
        int currentSum = 0; 
        int localStart = 0; 

        for (int i = 0; i < a.length; i++) { 
            currentSum += a[i]; 
            if (currentSum < 0) { 
                currentSum = 0; 
                localStart = i + 1; 
            } else if (currentSum > result[0]) { 
                result[0] = currentSum; 
                result[1] = localStart; 
                result[2] = i; 
            } 
        } 

        //all numbers in a are negative 
        if (result[2] == -1) { 
            result[0] = 0; 
            for (int i = 0; i < a.length; i++) { 
                if (a[i] > result[0]) { 
                    result[0] = a[i]; 
                    result[1] = i; 
                    result[2] = i; 
                } 
            } 
        } 

        return result; 
    } 

    /** 
    * To find and print maxSum, (left, top),(right, bottom) 
    */
    public static void findMaxSubMatrix(int[][] a) { 
        int cols = a[0].length; 
        int rows = a.length; 
        int[] currentResult; 
        int maxSum = Integer.MIN_VALUE; 
        int left = 0; 
        int top = 0; 
        int right = 0; 
        int bottom = 0; 

        for (int leftCol = 0; leftCol < cols; leftCol++) { 
            int[] tmp = new int[rows]; 

            for (int rightCol = leftCol; rightCol < cols; rightCol++) { 

                for (int i = 0; i < rows; i++) { 
                    tmp[i] += a[i][rightCol]; 
                } 
                currentResult = kadane(tmp); 
                if (currentResult[0] > maxSum) { 
                    maxSum = currentResult[0]; 
                    left = leftCol; 
                    top = currentResult[1]; 
                    right = rightCol; 
                    bottom = currentResult[2]; 
                } 
            } 
        } 
            System.out.println("MaxSum: " + maxSum + 
                                ", range: [(" + left + ", " + top + 
                                ")(" + right + ", " + bottom + ")]"); 
    } 
} 
// Thanks to Ilia Savin for contributing this code.
```

## Reference

* Youtube: [Maximum Sum Rectangular Submatrix in Matrix dynamic programming/2D kadane](https://www.youtube.com/watch?v=yCQN096CwWM)


---

# Agent Instructions
This documentation is published with GitBook. GitBook is the documentation platform designed so that both humans and AI agents can read, navigate, and reason over technical content effectively. Learn more at gitbook.com.

## Querying This Documentation
If you need additional information that is not directly available in this page, you can query the documentation dynamically by asking a question.

Perform an HTTP GET request on the current page URL with the `ask` query parameter, and the optional `goal` query parameter:

```
GET https://aaronice.gitbook.io/lintcode/data_structure/insert-delete-getrandom-o1.md?ask=<question>&goal=<endgoal>
```

`ask` is the immediate question: it should be specific, self-contained, and written in natural language.
`goal` is optional and describes the broader end goal you are ultimately trying to accomplish on behalf of the user. GitBook uses it to tailor the answer towards what is most useful for that goal.

The response will contain a direct answer to the question and relevant excerpts and sources from the documentation.

Use this mechanism when the answer is not explicitly present in the current page, you need clarification or additional context, or you want to retrieve related documentation sections.